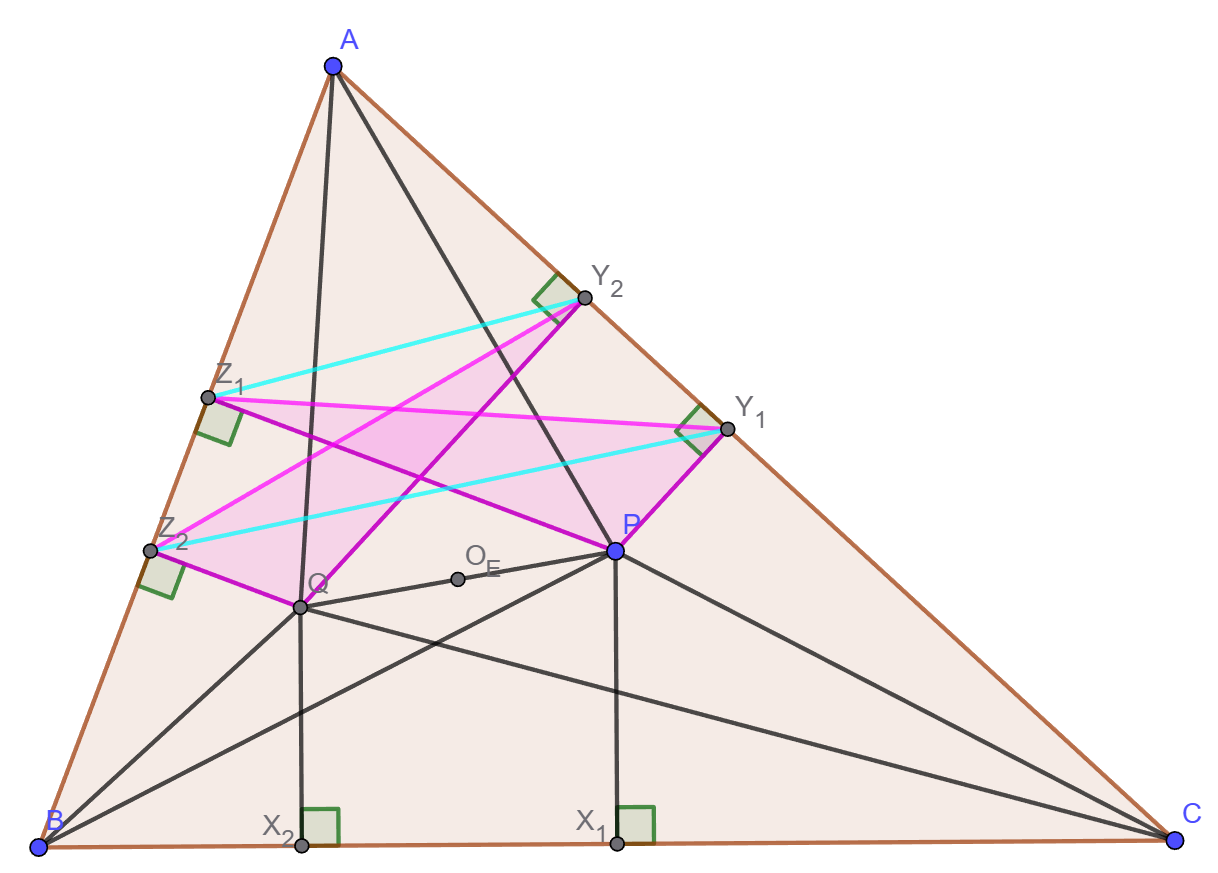
Primero notemos que la mediatriz de \overline{X_1X_2} corta a \overline{PQ} en su punto medio (al cual llamaremos O), análogamente tenemos que \overline{X_1O} = \overline{X_2O}, \overline{Y_1O} = \overline{Y_2O} \text{ y } \overline{Z_1O} = \overline{Z_2O}, esto evidentemente no nos basta para que el problema esté resuelto, pero será una herramienta sorpresa que nos ayudará más tarde.
Ahora demostraremos que los puntos Z_1, Z_2, Y_1 \text{ y } Y_2 son concíclicos. Notemos que los cuadrilateros PZ_1AY_1 y QZ_2AY_2 son cíclicos por lo ángulos de 90°, entonces \angle PZ_1Y_1 = \angle PAY_1 =\angle Z_2AQ = \angle Z_2Y_2Q y además \angle Y_2QZ_2 = 180° -\angle BAC = \angle Y_1PZ_1, por lo tanto \triangle Y_2QZ_2 \sim \triangle Z_1PY_1 por tex \Rightarrow \frac{Z_2Q}{Y_1P}=\frac{Y_2Q}{Z_1P}[/tex]. Notemos además que \triangle AZ_2Q\sim \triangle AY_1P \text{ y } \triangle AZ_1P \sim \triangle AY_2Q, entonces \frac{AZ_2}{AY_1}=\frac{Z_2Q}{Y_1P}=\frac{Y_2Q}{Z_1P} = \frac{AY_2}{AZ_1}\Rightarrow \overline{AZ_2}\cdot\overline{AZ_1}=\overline{AY_2}\cdot\overline{AY_1} por lo tanto el cuadrilátero Z_1Z_2Y_1Y_2 es cíclico. Como las mediatrices de \overline{Z_1Z_2} \text{ y }\overline{Y_1Y_2} se intersectan en O entonces \overline{Z_1O} = \overline{Z_2O} = \overline{Y_1O} = \overline{Y_2O}. Análogamente tenemos que \overline{Z_1O} = \overline{Z_2O} = \overline{Y_1O} = \overline{Y_2O} = \overline{X_1O} = \overline{X_2O} por lo tanto los puntos X_1, X_2, Y_1, Y_2, Z_1 \text{ y }Z_2 son concíclicos con O el centro de la circunferencia. \square