P1. [hide]Escribimos la suma de la forma: (10-1)+(10^2-1)+\ldots +(10^{2010}-1)=\underbrace{111\ldots 110}_{2010 \textrm{ veces}}-2010.
Luego los últimos cuatro dígitos quedan determinados por 11110-2010=9100.[/hide]
P2. [hide]Como el área del cuadrado mayor vale 64, entonces cada lado vale 8. Al dividirlo en razón 1 quedan triángulos rectángulos de catetos 2 y 6, cada uno de área 2\cdot 6 /2=6. Luego el área del cuadrado mediano es 64-4\cdot 6=40. De aquí se tiene que las áreas del cuadrado mediano y del mayor están en razón 5. Como el cuadrado menor se inscribe de la misma forma en el mediano que el mediano en el mayor, entonces está razón sigue siendo la misma. Por tanto, como el área del cuadrado mediano es 40, la del menor es 25.
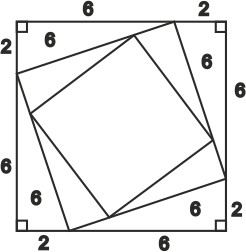
[/hide]
P3. [hide]Sean a,b,c,d las cuatro cifras (en el mismo orden) de un número que cumpla con las condiciones del enunciado, esto es, a\cdot b=d, a+b=c y a\cdot b\cdot c\cdot d=576.
De la primera y la tercera ecuación se obtiene c\cdot d^2=576=2^6\cdot 3^2. Como c y d son dígitos no es difícil ver que la única solución posible es c=9 y d=8.
Luego por las dos primeras ecuaciones se tiene que a=8 y b=1, ó a=1 y b=8. Es decir, los números buscados son 8198 y 1891.[/hide]