[b][center][size=3]IX CAMPEONATO ESCOLAR DE MATEMÁTICA - CMAT[/size]
Fecha 2: Sábado 14 de Mayo de 2011
Segundo Nivel Individual[/center][/b]
Problema 1
Encuentre todos los pares [tex](a,b) \in \mathbb{Z}[/tex] tal que:
[center][tex]a^2=b^2+p[/tex][/center]
Siendo [tex]p[/tex] un número primo ([tex]\neq 2[/tex]).
Problema 2
Dos triángulos [tex]ABC[/tex] y DEF están inscritos en la misma circunferencia de modo que [tex]AD[/tex], [tex]BE[/tex], y [tex]CF[/tex] concurren en [tex]I[/tex]. Demostrar que si [tex]I[/tex] es incentro del [tex]\triangle{ABC}[/tex] entonces [tex]I[/tex] es ortocentro del triángulo [tex]DEF[/tex] (recordamos que el incentro de un triángulo, es el punto del triángulo donde se intersectan las bisectrices interiores y el ortocentro de un triángulo es el punto donde se encuentran las alturas del triángulo).
[center]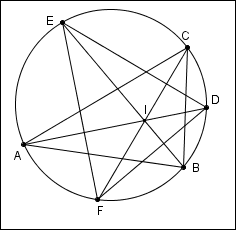
[/center]
