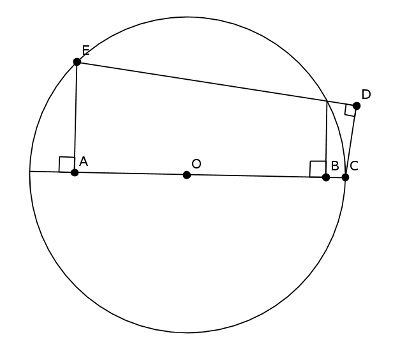
En la Figura, [tex]BC=a, AB=b[/tex]. Encuentre [tex]CD[/tex]
Una solución:
Probaremos que
[tex]ACDE\sim DCBF[/tex]
Para eso, probaremos que
[tex]\triangle CDE \sim \triangle CBF \qquad \text{y} \qquad \triangle ACE \sim \triangle DCF[/tex]
Tenemos que
[tex]\angle CDE \simeq \angle CBF[/tex]
Además
[tex]\widehat{FG} = 2 \cdot \angle BCF[/tex]
y como [tex]\angle BCF + \angle CFB = 90º[/tex], entonces [tex]\widehat{CF} = 2 \cdot \angle CEF[/tex] y [tex]\angle CEF + \angle BCF=90º[/tex]
Luego, [tex]\angle CEF \simeq \angle CFB[/tex], lo que implica que [tex]\angle DEC \simeq \angle CFB[/tex].
Por lo tanto, [tex]\triangle CDE \sim \triangle CBF\ \square[/tex]
Por otra parte:
[tex]\angle AED \simeq \angle BFD[/tex]
Por lo tanto, [tex]\angle AEC \simeq \angle DFC[/tex] y como [tex]\angle CDE \simeq \angle EAC[/tex], entonces [tex]\triangle ACE \sim \triangle DCF\ \square[/tex]
Hemos demostrado que [tex]ACDE\sim DCBF[/tex], por lo que se cumple que:
[tex]\frac{CD}{AB + BC} = \frac{BC}{CD}\Rightarrow CD^2 = BC \cdot (AB + BC) \Rightarrow CD = \sqrt{a \cdot (b + a)}[/tex]