En el triángulo [tex]ABC[/tex] de la figura, los catetos miden [tex]3[/tex] y [tex]4[/tex] .
Las circunferencias son iguales de radio [tex]R[/tex] , tangentes entre sí y tangentes con los lados del triángulo.
¿Cuánto vale [tex]R[/tex]?
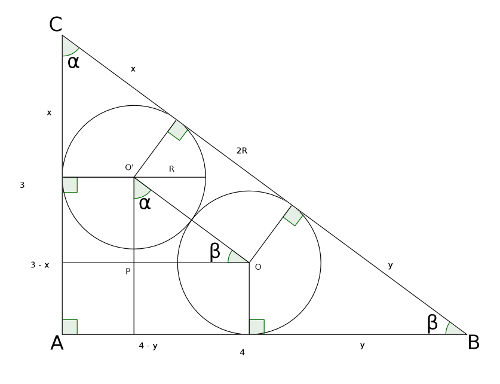
Una solución:
[tex]\overline{PO'} = 3x-R\quad ;\qquad \overline{PO} = 4 - y - R[/tex]
[tex]\alpha = \angle ACB = \angle PO'O[/tex]
[tex]\beta = \angle ABC = \angle POO'[/tex]
Entonces
[tex](3 - x- r)^2 + (4 - y -r)^2 = 4R^2[/tex]
Por semejanza
[tex]\frac{3 - x - R}{3} = \frac{4 - y - R}{4}[/tex]
[tex]\Rightarrow x = 3 - R - \frac{3}{4}(4 - y -R) \qquad (1)[/tex]
[tex]\Rightarrow \frac{25}{16}(4 - y - R)^2 = 4R^2[/tex]
[tex]\Rightarrow \frac{5}{4}(4 - y - R) = 2R[/tex]
[tex]\Rightarrow 20 - 5y = 13R[/tex]
[tex]\Rightarrow 13R + 5y = 20 \qquad \qquad \qquad \qquad (2)[/tex]
En la hipotenusa tenemos:
[tex]x + y + 2R = 5 \qquad \qquad \qquad \qquad (3)[/tex]
de (1) y (3)
[tex]3 - R - \frac{3}{4}(4 - y - R) + y + 2R = 5[/tex]
[tex]\Rightarrow y + R = \dfrac{20}{7} \qquad \qquad \qquad \qquad (4)[/tex]
de (4) y (2)
[tex]13R + 5(\frac{20}{7} - R) = 20[/tex]
[tex]\Rightarrow 8R = \dfrac{40}{7}[/tex]
[tex]R = \dfrac{5}{7}[/tex]