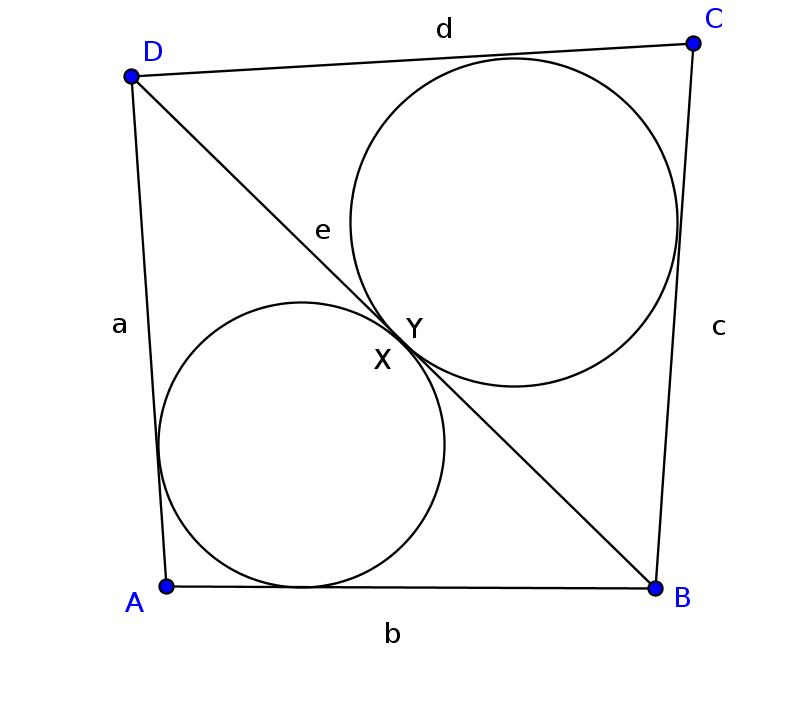
Una solución:
Sea [tex]a = AD, \quad b = AB, \quad c= BC, \quad d = CD \quad y \quad e = DB[/tex]
Sea [tex]X[/tex] el punto de tangencia de la circunferencia inscrita en el triángulo [tex]ABD[/tex] con [tex]DB[/tex].
Sea [tex]Y[/tex] el punto de tangencia de la circunferencia inscrita en el triángulo [tex]BCD[/tex] con [tex]DB[/tex].
Tenemos [tex]AX = \frac{a + e - b}{2}[/tex] y [tex]AY = \frac{d + e - c}{2}[/tex]
[tex]XY = AX - AY[/tex]
[tex]XY = \frac{a + e - b}{2} - \frac{d + e - c}{2}[/tex]
[tex]XY = \frac{a + c}{2} - \frac{b + d }{2}[/tex]
Por otra parte, como el cuadrilátero es circunscrito, se tiene [tex]a + c = b + d[/tex]
Por lo tanto [tex]XY = 0[/tex], entonces [tex]X = Y[/tex].
¡¡ Las cincunferencias son tangentes !!