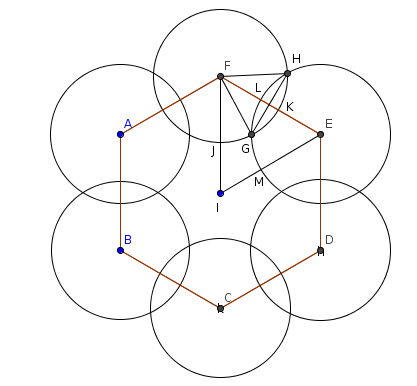
Una Solución:
El área pedida [tex]A[/tex] es [tex]6[/tex] veces el área IMGJ de la figura.
Tenemos:
[tex](IMGJ) = (\triangle IEF) - (ELM) - (FJK) + (KLG)[/tex]
donde:
[tex](\triangle IEF) =[/tex]
[tex]\frac{a²}{4}[/tex]
[tex]\sqrt{3}[/tex]
[tex](ELM) = (FJK) =[/tex]
[tex]\frac{\pi}{3}\frac{a²}{2}[/tex]
y
[tex](KLG) = \frac{(FGH) - (\triangle FGH}{2} =[/tex]
[tex]\frac{\pi}{2}\frac{a²}{2} - \frac{a²}{4} = \frac{a²}{4}[/tex]
[tex](\pi - 1)[/tex]
entonces
[tex](IMGJ) =[/tex]
[tex]\frac{a²}{4}[/tex]
[tex]\sqrt{3} -[/tex]
[tex]\frac{a²\pi}{3} + \frac{a²}{4}[/tex]
[tex](\pi - 1) =[/tex]
[tex]\frac{a²}{12}[/tex]
[tex](3\sqrt{3} - \pi - 3)[/tex]
Por lo tanto:
[tex]A =[/tex]
[tex]\frac{a²}{2}[/tex]
[tex](3\sqrt{3} - \pi - 3)[/tex]