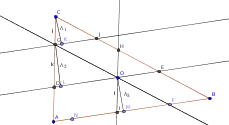
Una solución:
Tenemos que [tex]\triangle GJC \cong \triangle OEH[/tex].
y que
[tex]\triangle GJC \simeq \triangle ABC[/tex],
[tex]\triangle DOG \simeq \triangle ABC[/tex] y
[tex]\triangle IFO \simeq \triangle ABC[/tex], por lo tanto, se cumple:
[tex]\frac{h_1^2}{h_c^2} = \frac{(\triangle GJC)}{(\triangle ABC)}[/tex]
,
[tex]\frac{h_2^2}{h_c^2} = \frac{(\triangle DOG)}{(\triangle ABC)}[/tex]
,
[tex]\frac{h_3^2²}{h_c^2} = \frac{(\triangle IFO)}{(\triangle ABC)}[/tex]
.
entonces:
[tex]h_c = h_1 + h_2 + h_3 = h_c ( \frac{\sqrt{(\triangle GJC)}}{\sqrt{(\triangle ABC)}} + \frac{\sqrt{(\triangle DOG)}}{\sqrt{(\triangle ABC)}} + \frac{\sqrt{(\triangle IFO)}}{\sqrt{(\triangle ABC)}}[/tex], entonces
[tex](\triangle ABC) = (\sqrt{(\triangle GJC)} + \sqrt{(\triangle DOG)} + \sqrt{(\triangle IFO)})
²
[/tex]
[tex](\triangle ABC) = (2 + 3 + 4)² = 81[/tex]